Geometric V. Arithmetic Mean

From Dave McGlasson, does anyone have a reference on why a geometric mean is used in the INR calculation?  Since we are using 20–30 normal subjects to calculate the mean PT, the range is relatively narrow. The geometric mean indicates the central tendency or typical value of a set of numbers by using the product of their values as opposed to the arithmetic mean, which uses their sum. I have calculated several data sets side by side comparing both arithmetic and geometric means and have never seen a  clinically significantly difference that would require a physician to change a treatment plan.

The INR is faulty above 4.5 and should be considered semiquantitative. The curve flattens out. When comparing different reagent and instrument combinations the INR varies above 3.0.

I advocate doing away with the INR and going to using the chromogenic factor X (CFX) assay which reports the direct factor level. There are several studies that propose ranges for the CFX that correspond with the INR 2.0–3.0 therapeutic range and we don’t have to worry about a faulty formula.

Dave provides the figure of the left from Rosborough TK, Jacobsen JM, Shepherd MF. Relationship between chromogenic factor X and INR differs during early Coumadin initiation compared with chronic warfarin administration. Blood Coagul Fibrinolysis 2009 20:433-5. The figure illustrates the relationship between the CFX, X scale, and INR, Y scale. Notice that the INR and CFX diverge as the INR exceeds 3.0.

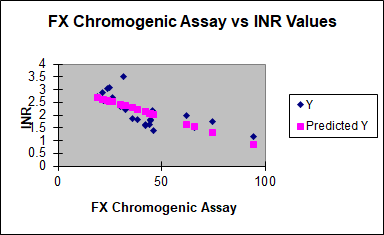
Likewise, the figure above, from McGlasson DL, Romick BG, Rubal BJ. Comparison of a chromogenic factor X assay with INR for monitoring oral anticoagulation therapy. Blood Coag Fibrinolys 2008;19:513–17, illustrates the irrelevance of INR values when compared to CFX results when the INR exceeds 3.0.